This post attempts to (in a half-mathematical, half-intuitive way)
- briefly explain zero-knowledge proofs and their definitions
- show an example with Schnorr's protocol for proving knowledge of discrete log
- introduce the integer commitment scheme of Damgard and Fujisaki (2001)
- introduce diophantine sets, and diophantine proof of knowledge (2003)
I'm also attempting to write a demonstration for this paper. (with additional assumptions and simplifications) Here's the link.
1. Zero Knowledge Proofs
Here's a very well-written introduction for zero-knowledge proofs by Matthew Green.
Zero-knowledge proofs are proofs that reveals nothing except for the assertion that the statement one is trying to prove is correct. For example, if I want to prove to a verifier that "I have this secret value $x$ satisfying some property", I want to do so without giving any extra information on $x$. At the same time, we want this proof to have the fundamentals of our intuition of a "proof" - that is, the verifier can be convinced of the proof if the statement is true, and the verifier can reject the proof if the statement is false.
To summarize, we want
- Completeness : If statement is true, the verifier properly following the protocol can verify the proof.
- Soundness : If statement is false, the verifier properly following the protocol can reject the proof with overwhelming probability.
- Zero-knowledge : If statement is true, the verifier learns nothing except for the fact that the statement is true.
We call people (prover, verifier) that are properly following a protocol to be honest.
We call people (prover, verifier) that are not properly following a protocol to be malicious.
For example, a malicious prover may want to forge a "proof" for a statement that is not true.
Also, a malicious verifier may want to extract some extra knowledge from the proof by not following the protocol precisely.
So we have this "learns nothing except for the fact that the statement is true" thing : how do we formalize it in mathematical terms?
The proofs we will deal in this writeup will be interactive proofs - proofs where the prover and verifier interact with each other to see whether the prover's claim is true of not. Also, the proof protocol will not be deterministic. Therefore the "proof script" - the complete interaction of the honest prover and verifier - will follow some distribution. If we simulate this proof protocol "precisely" by only using the statement that is being asserted, this will intuitively be a good definition of "zero-knowledge". Summarizing, we have two distributions :
- The distribution of the actual "proof script" between the honest prover and the verifier
- The distribution of the simulated "proof script" designed by only using the statement that is being asserted
Now we can truly define what it is to be "zero-knowledge" -
- Perfect Zero-Knowledge : No matter what verifier does, there's a simulated "proof script" that follows the exact same distribution with the actual "proof script" - so it is impossible to gather any extra knowledge, even with infinite computational resources
- Statistical Zero-Knowledge : The same as perfect zero-knowledge, but now the two distributions does not need to be the same - only "close". How do we determine if two distributions are close? Check out statistical distance.
- Computational Zero-Knowledge : The same, but the two distributions are computationally hard to distinguish.
- Honest-Verifier Zero-Knowledge : We now add the assumption that the verifier is honest.
- Prover generates a random $r \in [0, p)$ and sends $g^r$ to the verifier.
- Verifier issues a random challenge $c \in [0, p)$ and sends $c$ to the prover.
- Prover sends $z = (r + cx) \pmod{p}$ to the Verifier.
- Verifier checks if $g^z = g^r y^c$ is true. If not, the proof is false.
- They repeat the process until the probability that a malicious prover got away with a fake proof is small as desired.
- Completeness : If prover does know $x$, we see that $g^z = g^{r+cx} = g^r y^c$ is indeed true, so the verifier accepts it.
- Soundness : Here's an intuitive explanation that can be outlined to a proof. If some prover can answer the verifier's challenge with a high probability, the prover should know the value of $(r + cx) \pmod{p}$ for many values of $c$. From these values, one can easily recover the value of $x$. Therefore, we have proved that the prover must actually know $x$ in order to answer the challenges well.
- Zero-Knowledge : The actual proof script is $(g^r, c, (r + cx) \pmod{p})$ for i.i.d. $r, c \in [0, p)$. This is equal to the distribution of $(g^z y^{-c}, c, z)$ for i.i.d. $c, z \in [0, p)$. Therefore, we can perfectly simulate the proof script only using $g, y$ and the statement $g^x = y$.
This proves that the Schnorr's Protocol is honest-verifier perfect zero knowledge.
If the challenge is selected in $[0, 1]$ (binary challenge) the protocol can be proved to be perfect zero-knowledge.
- It is hard to generate a collision pair - i.e. $m \neq m'$ such that $H(m) = H(m')$.
- It is hard to find a preimage - i.e. given $H(m)$, it is hard to recover $m$.
- A small change in the message $m$ leads to a huge change in the hash $H(m)$.
Now what we can do is announce to the world that you have made a prediction with hash $H(m)$.
- Binding : Once you commit $m$, you cannot go back to another message $m'$.
- Hiding : No one can recover the value of $m$ from $H(m)$, so it hides the value of $m$.
Commitment schemes are of similar nature. Here, we will specifically look at integer commitment.
We want the cool properties of binding and hiding, and we want them to be defined clearly. Here's how we do it.
- Consider a deterministic commitment function $C$ that takes two integers as input.
- To commit an integer $x$, we generate a random integer $r$ and use $C(x, r)$ as our commitment value.
- The constraints on $x$ and the interval of $r$ to be selected from uniformly will be determined later.
- Binding : It is difficult to find $x, x', r, r'$ such that $x \neq x'$ and $C(x, r) = C(x', r')$.
- Hiding : For any $x, x'$, the distributions of $C(x, \cdot)$ and $C(x', \cdot)$ are equal/statistically close.
- Summation Protocol : If prover has three integers $a, b, c$ such that $a + b = c$ and their respective commitment $A, B, C$, they can prove that $a + b = c$ in a zero-knowledge way using only the commitment values $A, B, C$.
- Multiplication Protocol : If prover has three integers $a, b, c$ such that $ab = c$ and their respective commitment $A, B, C$, they can prove that $ab = c$ in a zero-knowledge way using only the commitment values $A, B, C$.
In other words, the prover can claim that "these commited values actually have this sum/product relation" in a zero-knowledge way.
It turns out that there is such a method, and it was devised by Damgard and Fujisaki in this paper.
To make explaining things much easier, we will cover only a part of the results shown in the paper. To be exact,
- We will only cover a specific case of the originally much, much more general construction of the scheme.
- We will not discuss the details of the proof of why the schemes are valid, but discuss some intuition & insights.
- Some protocols outlined below are not from the paper - these are mostly my thoughts & guesses.
- We will only consider the honest-verifier case - the transformation from honest-verifier case to the general case is dealt in the paper.
- The paper for Diophantine Argument of Knowledge also deals with extensions of this scheme. We do not deal with them here.
Now we discuss the actual scheme by Damgard and Fujisaki. We first need to describe the setup process.
- Setup - Part 1. The verifier takes two distinct, large safe primes $P, Q$ and let $n = PQ$. From the definition of safe primes, we can write $P = 2p+1$, $Q = 2q+1$ with $p, q$ being a prime. The verifier then constructs an element $h \in \mathbb{Z}_n^{\times}$ such that $h$ has order $pq$. From now on, we will work in the cyclic group $\langle h \rangle \le \mathbb{Z}_n^{\times}$ for our commitments.
- Setup - Part 2. Assume that $n$ is a $k$-bit modulus - then anyone who knows $n$ also knows that the cyclic group generated by $h$ has order less than $2^B$ for $B = k$. This is an important piece of information for statistical zero-knowledge.
- Setup - Part 3. The verifier generates $\alpha$ randomly from $[0, 2^{B+k})$, and sets $g = h^{\alpha}$. The verifier sends $n, g, h$ to the prover, and the verifier proves the knowledge of $\alpha$ such that $g = h^{\alpha}$ in a zero-knowledge way. This can be done with a binary challenge process similar to Schnorr's protocol. It's important to note that since factorizing $n$ is hard, the prover does not know the order of $h$.
- Note that the prover also knows the values of $B$ and $k$, since they can be easily derived from $n$.
- Setup - Part 4. We also need an additional parameter $C$ - an higher value of $C$ will result in lower error probability, but at the same time we need $C$ to satisfy one of our assumptions below. Because we are dealing with a specific case of a much general construction in the paper, setting $C$ as high as $pq$ is not an issue. For more insight on selecting $C$, it is recommended to refer to the original paper.
Now that we know what we are working with - integers modulo $n$ as commitment, we can outline some assumptions.
While there are actually more assumptions involved, using the safe prime construction only leaves us with two -
- Strong Root Assumption : Basically, if one is given a random $y \in \langle h \rangle$, then it is hard to find $x \in \langle h \rangle$ and $t \ge 2$ such that $y = x^t$.
- Small Order Assumption : Basically, it is hard to find a $\sigma$ and $b \in \langle h \rangle$ such that $0 < \sigma < C$ and $b \neq 1$ and $b^\sigma = 1$.
In the safe prime construction, we can just replace the two with the Strong RSA assumption, alongside with a suitable value of $C$.
Now we discuss how to commit integers. To commit an integer $x$, the prover selects some $r \in [0, 2^{B+k})$ and makes a commitment as $C(x, r) = g^x h^r$. It can be proved that this commitment scheme has the (statistical) hiding property and the binding property.
Also, from now on, we assume that the integers being commited are in some finite interval $[-T, T]$. This is a required assumption for proofs to be zero-knowledge. Of course, a malicious prover can try to commit integers that are not in this interval - therefore, the verifier must also ask for a proof that the integer is indeed in this interval. The method for this "range proof" will be outlined in the next section.
Now we discuss the proofs between the prover and the verifier. There are many things we want to prove, these include
- Proving you know how to open : Assume the prover has some integer $x$ and its commitment $C$. The prover now wants to prove the knowledge of $x, r$ such that $C = C(x, r)$ - can it be done without leaking information on $x, r$?
- Summation Protocol : If prover has three integers $a, b, c$ such that $a + b = c$ and their respective commitment $A, B, C$, they can prove that $a + b = c$ in a zero-knowledge way using only the commitment values $A, B, C$.
- Multiplication Protocol : If prover has three integers $a, b, c$ such that $ab = c$ and their respective commitment $A, B, C$, they can prove that $ab = c$ in a zero-knowledge way using only the commitment values $A, B, C$.
Proving you know how to open
- Keynotes : We imitate Schnorr's protocol - but the range we choose our parameters from needs to be selected carefully.
- Step 0. Prover has some commitment $C = C(x, r)$ and would like to prove they know how to open.
- Step 1. Prover chooses some random $y \in [0, TC 2^k)$ and $s \in [C 2^{B+2k})$, sends $d = g^y h^s$.
- Step 2. The verifier issues a challenge $e \in [0, C)$ and sends it to the prover.
- Step 3. Prover sends $u = y + ex$ and $v = s + er$ - verifier checks $g^u h^v = dc^e$
Summation Protocol
- Keynotes : The key is that if $A = g^a h^{r_1}$, $B = g^b h^{r_2}$, $C = g^c h^{r_3}$ with $a + b = c$, we know the discrete logarithm of $C(AB)^{-1} = h^{r_3-r_1-r_2}$ over base $h$. Since the prover cannot calculate the discrete logarithm of $g$ over $h$, this can be a proof.
- Step 0. Prover has three commitments $A, B, C$ of $a, b, c$ and would like to prove $a + b = c$.
- Step 1. Prover first proves that they can open the commitments $A, B, C$ in a zero-knowledge way.
- Step 2. Prover then proves the knowledge of discrete logarithm of $C(AB)^{-1}$ over base $h$ in a zero-knowledge way. Since we have assumed honest-verifier setting, it can be done in a way similar to Schnorr's protocol. Of course, we have to be careful about the range we choose our parameters from. The same applies for the Setup stage, where the verifier proves the knowledge of $\alpha$ to the prover. For details, refer to the original paper, page 5. This completes the proof of $a + b = c$, in a zero-knowledge way.
Multiplication Protocol
- Keynotes : The key is that if $A = g^a h^{r_1}$, $B = g^b h^{r_2}$, $C = g^c h^{r_3}$ with $ab = c$, we have $C = A^b h^{r_3 - br_1}$.
- Step 0. Prover has three commitments $A, B, C$ of $a, b, c$ and would like to prove $ab = c$.
- Step 1. Prover chooses random $y \in [0, TC2^k)$, $s_2 \in [0, C 2^{B+2k})$, $s_3 \in [0, TC2^{B+2k})$.
- Step 2. Prover sends $d_2 = g^y h^{s_2}$, $d_3 = A^y h^{s_3}$ to the verifier.
- Step 3. Verifier issues challenge $e \in [0, C)$ and sends it to the prover.
- Step 4. Prover sends $u = y + eb$, $v_2 = s_2 + er_2$, $v_3 = s_3 + e(r_3 - br_1)$ to the verifier.
- Step 5. Verifier checks if $g^u h^{v_2} = d_2 B^e$, $A^u h^{v_3} = d_3 C^e$ holds.
We will now (very) briefly sketch how the each protocols are proved to be zero-knowledge. The stuff going on is basically
- Proving Completeness : Trivial - just substitute all values in and check if the equation is true.
- Proving Soundness : "Standard proof techniques for soundness" + Assumptions (Strong Root, Small Order, Strong RSA, etc)
- Proving Zero-Knowledge : Done by simulation - the choice of the intervals in which we select our parameters comes into play here.
- Additional Notes : It's very important that the prover does not know the order of $h$ - for example, if the prover knew the order $pq$, they can forge a commitment of $x$ into a commitment of $x + pq$ easily. However, this condition makes it hard for the prover to truly generate a "uniform random distribution" (for example, in Schnorr's protocol, the prover generates the integer in $[0, p)$, where $p$ is the group order) - and this is why we need statistical zero-knowledge instead of the "perfect" variant. It's quite tricky...
4. Diophantine Sets and Diophantine Argument of Knowledge
Now let's think about what we can do with our integer commitment scheme. Working with integers in $[-T, T]$, we can
- Prove $a + b = c$ with only commitments, in a zero-knowledge way.
- Prove $ab = c$ with only commitments, in a zero-knowledge way.
It's clear that by using addition and multiplication protocols we can actually prove that we have computed an integer coefficient multivariable polynomial on some input. In other words, we can prove that $y = f(x_1, x_2, \cdots , x_n)$, for some integer coefficient polynomial that both prover & verifier know using only the commitment values for $x_i$'s and $y$ in a zero-knowledge way. Here's an easy example.
- Prover has some values $x_1, x_2, x_3, x_4$ that satisfies $x_4 = x_1x_2 + x_3$. How to prove it?
- Prover calculates $x_5 = x_1x_2$ and commits $x_1, x_2, x_3, x_4, x_5$.
- Prover can now prove $x_5 = x_1x_2$ and $x_4 = x_3 + x_5$ in a zero-knowledge proof, only using commitments.
While that's cool and already has quite a lot of applications, it's quite limited. There are plenty of prepositions that one would like to prove that does not have the form of "I evaluated a integer coefficient polynomial"... - or are there?
To dig deeper here, we need the notion of Diophantine Sets.
- Diophantine Sets : A set $S \subset \mathbb{Z}^k$ is called Diophantine if and only if there exists a integer coefficient multivariate polynomial $P$ such that $v \in S \iff \exists w \in \mathbb{Z}^{k'} \text{ s.t. } P(v, w) = 0$, i.e. if $v \in S$ iff $v$ is a part of a solution for a fixed Diophantine equation.
- In the above definition, we call $P$ as a representing polynomial of $S$, and $w$ as a witness.
This notion leads us to a much more versatile approaches for a proof. If $S$ is Diophantine and I want to prove $v \in S$, I can
- Find a representing polynomial $P$ of $S$ and publicize it along with the full formula & proof for $P$.
- To prove $v \in S$, find a witness $w$. Prove $P(v, w) = 0$ using integer commitment scheme.
This is the fundamental idea of Diophantine Argument of Knowledge, abbreviated as DARK.
The obvious question is "what sets are Diophantine?" : after all, it should cover a lot of different sets for this to have practical meaning.
Here's one of the more surprising results in mathematics -
- Computably Enumerable Sets : A set $S$ is computably enumerable if and only if there is an algorithm that halts if the input is a member of $S$, and runs forever if otherwise. Equivalently, a set $S$ is computably enumerable if there is an algorithm (not necessarily halts) that enumerates the members of $S$. Obviously, a lot of sets we deal with are computably enumerable.
- Matiyasevich's Theorem (MRDP Theorem) : [Diophantine Sets] = [Computably Enumerable Sets]
so a metric ton of sets are Diophantine. However, to put into practical use, more questions must be asked.
- How do we even find the suitable representing polynomial $P$? How do we prove it?
- If we found $P$, how do we find the witness $w$? Is the size (number of bits) of $w$ reasonable/practical?
Therefore, we deal with special Diophantine sets that
- have representing polynomial $P$ (we can actually construct)
- has a polynomial time algorithm to compute the witness $w$, which has polynomial length.
In this paper, we narrow down our choices even further, by adding the constraint
- the length of our witness has to be subquadratic to the length of the input
which is important for practical uses. Now our question is "what can we prove under these constraints?".
5. Tricks, Range Proofs, Exponential Relations, and Bounded Arithmetic
Tricks
Here we outline some tips and tricks that we will use later on. Suppose we have two Diophantine sets $S_1$ and $S_2$, with respective representing polynomials $P_1, P_2$. How do we deal with $S_1 \cap S_2$ or $S_1 \cup S_2$? These will be our way to deal with and/or operations on prepositions.
- $S_1 \cap S_2$ : We use $P_{\cap}(v, w_1, w_2) = P_1(v, w_1)^2 + P_2(v, w_2)^2$ as our polynomial.
- $S_1 \cup S_2$ : We use $P_{\cup}(v, w_1, w_2) = P_1(v, w_1) \cdot P_2(v, w_2)$ as our polynomial.
It's relatively clear that these two work as desired, and witnesses can be transported over as well.
Range Proofs
We have a homework from chapter 3 - we have to prove a value is in some range for the scheme to work.
To prove $-T \le x \le T$, it suffices to prove $T-x \ge 0$ and $T+x \ge 0$. Therefore, it suffices to have a scheme that proves an integer is nonnegative. To do this, it suffices to have a nice representing polynomial $P$ for nonnegative integers, with witness easy to find.
- Construction : We use the polynomial $P(x, a, b, c, d) = x - a^2 - b^2 - c^2 - d^2$.
- Proof (representation) : Obviously, if $P(x, a, b, c, d) = 0$, we have $x = a^2 + b^2 + c^2 + d^2 \ge 0$. On the other hand, if we have $x \ge 0$, we can write it as $a^2 + b^2 + c^2 + d^2$ by Lagrange's Four Square Theorem.
- Proof (efficiency) : It is clear that the witness size is not an issue here. We show that it's feasible to find $a, b, c, d$ such that $a^2 + b^2 + c^2 + d^2 = x$. A quick outline of an (probabilistic) algorithm is as follows -
- Algorithm : If $x$ is small, we can simply brute force over $a, b, c, d \in [0, \sqrt{x}]$. If $x$ is large, take $c$ as a random value in $[0, \sqrt{x}]$ and $d$ as a random value in $[0, \sqrt{x-c^2}]$. Now, we pray that $x - c^2 - d^2$ is actually a prime of the form $4k+1$. Heuristically, with Prime Number Theorem, we can see that there exists a good probability that this holds. Now all we need to do is write $x-c^2-d^2$ as a sum of two squares. There exists a few fast algorithms that writes a $4k+1$ prime as a sum of two squares - check out this cool thread.
Now we can argue stuff like $a \ge b$ in our proofs, and it gives us much more versatility!
Exponential Relations
Here, our goal is to prove $c = a^b$. Our views on representation polynomial are a bit different since we now have a view that is focused on practical applications - we will change it as follows. This turns out to be important for proving $c = a^b$ zero-knowledge.
- If $v \in S$, we should be able to efficiently find a polynomial length $w$ such that $P(v, w) = 0$.
- If $v \notin S$, we should not be able to efficiently find a polynomial length $w$ such that $P(v, w) = 0$ - one way to prove this "not able to efficiently find" thing, is to prove that all the fake "witness" $w$ with $P(v, w) = 0$ has very large length.
We can now enjoy the following theorem, and I will not even try to type this out or code this.
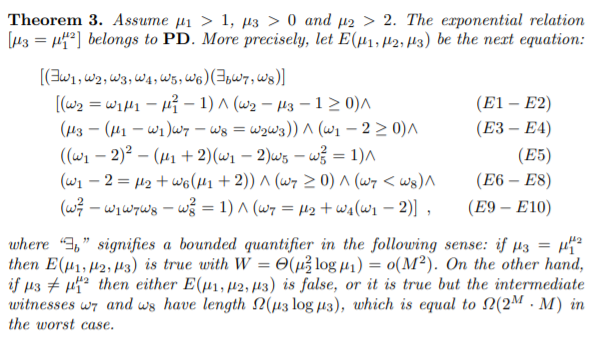
Let's decipher this. Since the expressions (E1-E10) are all prepositions that can be written as a polynomial equation, we can combine them as a one big integer coefficient multivariate polynomial $P$ with our "trick". Basically, if $\mu_1^{\mu_2} = \mu_3$, we can efficiently find our witness for $P$ that has subquadratic length. If $\mu_1^{\mu_2} \neq \mu_3$, either the witness for $P$ does not exist, or the witness has a large length, $\Omega(\mu_3 \log \mu_3)$ - which makes it impractical to use as a fake "proof" that $\mu_1^{\mu_2} = \mu_3$. We can also take care of edge cases like $\mu_1=0, 1$, $\mu_2 = 0, 1, 2$, $\mu_3=0$ easily with our "trick" as well. This shows that we can completely prove $a^b = c$ with DARK, zero-knowledge.
Bounded Arithmetic
Now that we have a lot of tools at hand, we can take a look at what we can do.
- Bounded Arithmetic : We work over the nonnegative integers, and only use the following operations
- $0$, $\sigma$, $+$, $\cdot$, $\le$, $-$, $|x|$, $\lfloor x/2 \rfloor$, $\lfloor x/2^k \rfloor$, $\sharp$
- $0, +, \cdot , \le , \lfloor x/2 \rfloor , \lfloor x/2^k \rfloor$ have usual definitions.
- $\sigma(x)$ is simply $x$'s next integer, $x + 1$.
- $-$ is a bit different because we are working over nonnegative integers, $x-y$ is actually $\max(x-y, 0)$.
- $|x|$ is the bitwise length of $x$, i.e. $\lfloor \log_2 (x) \rfloor + 1$, excluding the case $x = 0$. $x \sharp y$ is defined as $2^{|x| \cdot |y|}$
Since we now have and/or of prepositions, addition, multiplication, exponentiation ready to be proved in a zero-knowledge way, we can combine these with relative ease to show that all of those operations can be used, and proved in a zero-knowledge way. It seems that bounded arithmetic is quite researched, and a lot of useful prepositions can be written using the bounded arithmetic language.
Here's an outline of proof -
- $0, +, \cdot$ : We already know how to prove these by our integer commitment scheme.
- $ \le $ : We studied how to do range proofs - simply proof $b - a \ge 0$ to show $a \le b$.
- $ - $ : $a - b = c$ is either ($a = b+ c$ and $c \ge 0$) or ($a \le b$ and $c = 0$), so combine.
- $|x|$ : Deal with the case $x=0$ separately, and write $y = |x|$ as $2^{y-1} \le x \le 2^y-1$. Now do range proofs & exponentiation.
- $\lfloor x/2 \rfloor$ : $y = \lfloor x/2 \rfloor$ is simply $x = 2y$ or $x = 2y + 1$, so combine them.
- $\lfloor x/2^k \rfloor$ : $y = \lfloor x/2^k \rfloor$ is simply $x = 2^ky + z$ and $0 \le z \le 2^k-1$, so combine them.
- $\sharp$ : Since we can do proofs for $|x|$ and proofs for exponentiation, combining is quite trivial.
There are definitely more content in this paper, including some practical applications and reduction of proof size.
There's also a relatively new paper in 2019 that is much harder and very interesting. Might try to read this one...
'Cryptography' 카테고리의 다른 글
| Sigma Protocol (0) | 2021.02.15 |
|---|---|
| Schnorr's Protocol & Signature (0) | 2021.02.13 |
| Leftover Hash Lemma and its Applications (0) | 2020.10.18 |
| 암호론 논문 리딩 #4: The Return of Coppersmith’s Attack: Practical Factorization of Widely Used RSA Moduli (0) | 2020.06.25 |
| 암호론 논문 리딩 #3: Twenty Years of Attacks on the RSA Cryptosystem (1) | 2020.04.02 |