I played GoogleCTF Quals as a member of Super Guesser. We reached 9th place, which is good enough for a place in the Finals!
I solved all five cryptography problems, one (pythia) with barkingdog. While this was good work, I'm still sad that I couldn't solve the misc "cryptography" problem due to lack of time and creativity (and probably work ethic as well). Here's how we solved the cryptos.
NOTE : All challenges from GoogleCTF are open sourced, so check them here. https://github.com/google/google-ctf/tree/master/2021
exploit codes for all five challenges can be found on https://github.com/rkm0959/Cryptography_Writeups/tree/main/2021
tiramisu (28 solves)
Step 1 : Basic Analysis
We start by reading some golang codes. We see that the code roughly does the following
- We receive the server's ECDSA public key and the encrypted flag message.
- The flag is encrypted with AES, using the key derived by HMAC with the ECDSA secret key.
- We can send our ECDSA public key, which would normally allow us to compute the shared secret.
- Using this shared secret, we send an authenticated encrypted message to the server.
- The server checks if we sent a valid encryption, and replys with another valid encryption with different IV.
Step 2 : Reducing the Problem and Finding Attack Vector
First, note that HMAC with a strong hash like sha256 is very hard if not impossible to break.
Therefore, we should probably look deeper into the inner workings of the ECDSA implementation.
Especially, since the flag is encrypted with a HMAC-derived key, we must recover ECDSA secret key at some point.
This immediately implies that the following message is a very scorching hot take.

After realizing that people are actually solving this problem, we look more into the ECDSA.
We see that there are actually two curves supported in this implementation, as shown in this code.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
func (server *Server) EstablishChannel(clientHello *pb.ClientHello) error {
// Load peer key.
peer, err := proto2ecdsaKey(clientHello.Key)
if err != nil {
return err
}
// Key sanity checks.
if !peer.Curve.IsOnCurve(peer.X, peer.Y) {
return fmt.Errorf("point (%X, %X) not on curve", peer.X, peer.Y)
}
// Compute shared secret.
P := server.key.Params().P
D := server.key.D.Bytes()
sharedX, _ := server.key.ScalarMult(new(big.Int).Mod(peer.X, P), new(big.Int).Mod(peer.Y, P), D)
masterSecret := make([]byte, server.key.Params().BitSize/8)
sharedX.FillBytes(masterSecret)
// Derive AES+MAC session keys.
server.channel, err = newAuthCipher(masterSecret, channelCipherKdfInfo, channelMacKdfInfo)
if err != nil {
return fmt.Errorf("newAuthCipher()=%v, want nil error", err)
}
return nil
}
|
cs |
Now we see the vulnerability! The server checks our point lies on our curve, but then takes the coordinates modulo $P$, which is the modulo from the server's curve. Since there are no restrictions on the coordinate size, by Chinese Remainder Theorem, we have a complete control over the final coordinates taken modulo $P$. The server takes this faulty point and multiply it by $D$, the ECDSA secret key.
Step 3 : The Invalid Curve Attack
Turns out that the problem now reduces to a known attack called the invalid curve attack.
Basically, when we work on the Weierstrass curve $y^2 = x^3 + ax + b$, the standard implementations for adding and doubling points never uses the value of $b$. It only uses the value of $a$ and the one or two points of the input.
Therefore, if the server considers a point $(X, Y)$ and considers it as a point on $y^2 = x^3 + ax + b$ while multiplying a scalar to it, it actually performs valid scalar multiplication, although the computation is on the point $y^2 = x^3 + ax + b'$, where $$b' \equiv Y^2 - X^3 - aX \pmod{p}$$
Since we have full control on $(X, Y)$, the result after the coordinates are taken modulo $P$, we can actually select any curves of the form $y^2 = x^3 - 3x + b$. To exploit this even further, we can use the small subgroup attack. Consider we take find a curve $y^2 = x^3 - 3x + b$ which has an order which is a multiple of a small prime $m$. We can then take a point $(X, Y)$ on this curve with order $m$. If we send this point, the shared secret will be the first coordinate of a scalar multiple of $(X, Y)$, which there are only at most $m$ candidates.
Since we can easily determine if our guess for a shared secret is valid by checking whether we receive a reply or not, we can test all $m$ candidates. However, the shared secret is just the first coordinate of the elliptic curve point. This means we will actually get two possible candidates for $D \pmod{m}$, so something like $D \equiv \pm l \pmod{m}$, since the additive inverse of a point has the same first coordinate.
If we gather a lot of such information, we will be able to find a sufficiently small candidates for $D$ by Chinese Remainder Theorem.
To do so, we choose the "signs" in each modulo relation, compute $D$ by Chinese Remainder Theorem, and repeat.
Step 4. Implementation and Finish
- Choosing the Modulo $m$ - Prime : I chose the modulo $m$ to be prime, since they give a lot of information in a sense that $m$ will have GCD 1 with all the previous modulos I used. If you get $\pmod{m_1}$ and $\pmod{m_2}$ information, then you will get $\pmod{\text{lcm}(m_1, m_2)}$ information in total by Chinese Remainder Theorem. Therefore, having $\gcd(m_1, m_2) = 1$ usually helps.
- Choosing the Modulo $m$ - Size : This is quite important. If we take larger $m$, the number of modulo relations we need to take becomes smaller. This implies that we have an easier offline bruteforce of choosing signs, computing Chinese Remainder parts, and either ECDSA public key verification or AES decryption. However, choosing larger $m$ also implies that we have to search more elliptic curves to find a appropriate one, and we also need to interact with the server more to decide what $D \pmod{m}$ can be. If we take small $m$, everything becomes the opposite. I chose $m$ to be a prime between $300$ and $1000$. In my case, 25 relations were sufficient to find $2^{25}$ candidates for $D$, which is definitely a feasible number of candidates for final offline bruteforce.
- Multiprocessing : I used it to speedup both the server computation and the offline bruteforce.
- Trick from rbtree : Instead of bruteforcing the signs, one can just solve for $D^2$ by CRT and take sqrt. In this case, you would need twice more information on $D \pmod{m}$, but you don't need the extra bruteforce. Great idea from rbtree, shared after contest!
pythia (65 solves)
This was a tricky problem for me, as I found the solution nearly immediately but struggled to write the exploit.
Step 1 : Basic Analysis
- There are a total of $26^3$ possible passwords, each corresponding to a 16 bytes AES-GCM key.
- There is a password (key) we have to find. We must do it using around 48 queries of the following type.
- We can send some nonce/ciphertext/tag to be AES-GCM decrypted with the key without any associated data.
- The only response we get from the queries are whether or not the decryption process was successful.
Note that there are actually 150 queries and 3 passwords, but since each three problems are independent, we can just focus on one.
Step 2 : Reducing the Problem and Finding Attack Vector
In these types of problems, it's best to halve the number of candidates by each query.
To do so, we have to figure out how to build some nonce/ciphertext/tag that accepts all of the keys from a given set.
If we can do this, we can simply perform a "binary search" to get each password. This is a good time to look at how AES-GCM works.
Step 3 : AES-GCM and Polynomial Fun
Here, we only consider the case where there are no associated data and we have 12 byte nonce. Everything is in $GF(2^{128})$.
Let $K$ be the key, $C = C_0 || C_1 || \cdots || C_{n-1}$ the ciphertext, and $IV$ the nonce. We now calculate $$H = AES_K(0^{128}), \quad J_0 = IV || 0^{31} || 1, \quad L = 0^{64} || len(C)$$
The tag $T$ is now calculated as $T = C_0 H^{n+1} + C_1 H^n + \cdots + L \cdot H + AES_K(J_0)$.
Let's fix $IV= 0^{96}$. If we know $K$ and $n$, then we can calculate $H, J_0, L, AES_K(J_0)$.
Now we want the polynomial coefficients $C_0, C_1, \cdots, C_{n-1}, T$ such that $$C_0 H^{n+1} + C_1 H^n + \cdots + L \cdot H + T = AES_K(J_0)$$ for a given set of $K$. To be exact, if we have $K_1, K_2, \cdots , K_m$ as a target set of keys, we compute the corresponding $H_1, H_2, \cdots , H_m$.
Then, we will try to find $n, C_0, C_1, \cdots , C_{n-1}, T$ such that $$C_0 H_t^{n+1} + C_1 H_t^n + \cdots + C_{n-1} H_t^2 + L H_t + T = AES_{K_t}(J_0)$$ for each $1 \le t \le m$. This is starting to look like Lagrange interpolation, with the caveat that $L$ is determined by $n$.
Take $n=m$. Let $f(x) = C_0 x^{m+1} + \cdots + C_{m-1} x^2 + L x + T$, which is a polynomial we want to find.
Our desired $f$ must satisfy $f(H_t) = AES_{K_t}(J_0)$ for each $1 \le t \le m$.
This $f$ can be found directly with Lagrange interpolation, and $f$ will have degree at most $m-1$. However, we have to set $f$'s coefficient of $x$ to be equal to $L$. This can be done by adding some scalar multiple of $g = (x-H_1)(x-H_2) \cdots (x-H_m)$.
However, if this $g$ has the coefficient of $x$ equal to $0$, we cannot control this coefficient by adding $g$.
In this case, we have to control it by multiplying some random degree 1 polynomial.
Finally, note that we can put any number of zero blocks at the front of the ciphertext to meet the length requirement if $\deg f < m+1$.
There are a lot of methods to handle these sepcial cases, (i.e. $g$ can't control the coefficient) and the solution writeen by barkingdog is a bit different from what I wrote as well. He handled these cases by simply adding a few random points for the interpolation part of $f$.
This makes $g$ and it's coefficients much more random, making it unlikely for the coefficient to be zero.
I would like to note that is error is a very unlikely case, so not error-handling these special cases won't hurt.
Step 4 : Implementation Details
- Fast Interpolation : If we try to find $C_i, T$ with a system of linear equations, the algorithm will take $\mathcal{O}(n^3)$ time which is quite slow. A relatively naive lagrange interpolation takes $\mathcal{O}(n^2)$ time. I suggest just using SageMath's lagrange polynomial function.
- Binary Search : If we just use standard binary search, we would have to compute $f$ for a set of $26^3/2$ keys. This is quite large for us to handle, and it may not even fit the payload size. Since we have much more than $\log(26^3) < 15$ queries per password, we can try to make our interpolation computation easier at the cost of using more queries. Here is one way to do so - we divide the set of $26^3$ keys into $40$ batches of size around $440$. We find which batch the key is in, and then use standard binary search. This fits in the query limit quite tightly. Note that if we found the batch that has the key, we do not need to check the other batches.
- Cache : Note that the payload to test whether the key is in a certain set can be precomputed beforehand. Therefore, by using a cache or hashmap or whatever, we can save ourselves from repeating the same computation over and over again. This is especially useful when we are testing the $40$ batches - we will test the same batches for all three passwords, and computing the payload for all of them takes quite a while. By saving these payloads, we can save quite a lot of time on the exploit.
- AES-GCM : endian stuff are very confusing to figure out, so you have to really concentrate
h1 (23 solves)
Step 1 : Basic Analysis
- We have some ECDSA looking stuff (it's actually just elliptic curve operations with Jacobians)
- We have some signatures, but we do not know any public key.
- Alice has sent two messages and signatures, but one of the messages contain the unknown flag.
- Bob has sent two messages and signatures, and we know both messages and their hashes.
- We also know the AES encrypted messages (one contains flag) with the shared secret as the key.
- The ECDSA nonce is yelling loudly at us to attack it which we obviously have to do.
Step 2 : Reducing the Problem and Finding Attack Vector
Obviously there is something going on with the custom RNG, and it becomes apparent if we read the code.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def RNG(nbits, a, b):
nbytes = nbits // 8
B = os.urandom(nbytes)
return a * sum([B[i] * b ** i for i in range(len(B))]) % 2**nbits
def Sign(msg, d):
h = hashlib.sha512(msg)
z = Transform(int.from_bytes(h.digest(), 'big'), h.digest_size*8)
k = RNG(n.bit_length(), 16843009, 4294967296)
x1, y1, z1 = Multiply(G, k)
r = (x1 * pow(z1, -2, mod) % mod) % n
s = pow(k, -1, n) * (z + r * d) % n
return r, s
|
cs |
We see that $n$ is $512$ bits, and our RNG call uses $b = 2^{32}$. Therefore, in the RNG call, the nonce can be written as $$ \sum_{i=0}^{15} a \cdot byte_i \cdot 2^{32i}$$ since all values from $i \ge 16$ becomes $0$ modulo $2^{512}$. Note that $255a < 2^{32}$, so no modulo operations are needed.
Since each $byte_i$ has 8 bit of "entropy", in total the RNG has only 128 bits of "entropy", which is horrible.
This also means that each complete message/signature pair gives us around 384 bits of information on the secret key.
Since we have two such pairs for Bob's secret key $db$, we should be able to extract this value.
Clearly, computing the shared secret solves the problem, so we just need the public key of Alice.
This is not hard, as given one complete message/signature you can recover the public key. This is even in wikipedia.
NOTE : There may be more than one public key possible, so try all of them to find the flag.
Therefore, clearly getting the secret key $db$ is the hardest part of the challenge, unless you are rkm0959 who doesn't know fundamentals.
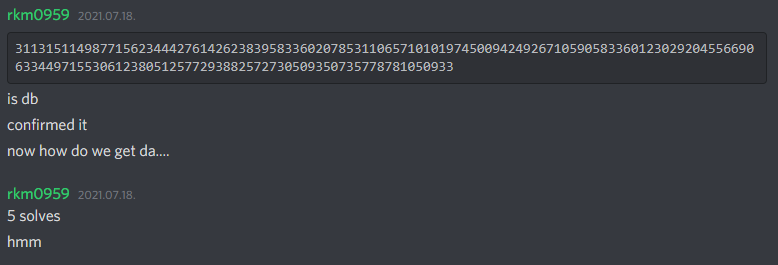
Step 3 : Yet Another Inequality Solving with CVP!
Consider the message, signature pair $(r_1, s_1, z_1)$ and $(r_2, s_2, z_2)$, where $z$'s are the hashes. We know $$ \left( \sum_{i=0}^{15} a \cdot byte_{1, i} \cdot 2^{32i} \right) \cdot s_1 \equiv z_1 + r_1 d \pmod{n}$$ $$ \left( \sum_{i=0}^{15} a \cdot byte_{2, i} \cdot 2^{32i} \right) \cdot s_2 \equiv z_2 + r_2 d \pmod{n}$$ Since we can, we will remove $d$ from this system by writing $$ \left( \sum_{i=0}^{15} a \cdot r_2 \cdot byte_{1, i} \cdot 2^{32i} \right) \cdot s_1 - \left( \sum_{i=0}^{15} a \cdot r_1 \cdot byte_{2, i} \cdot 2^{32i} \right) \cdot s_2 \equiv z_1r_2 - z_2r_1 \pmod{n}$$ Now we can consider $33$ variables $byte_{1, i}, byte_{2, i}, t$ for $0 \le i \le 15$, and use the $33$ inequalities $$\left( \sum_{i=0}^{15} a \cdot r_2 \cdot byte_{1, i} \cdot 2^{32i} \right) \cdot s_1 - \left( \sum_{i=0}^{15} a \cdot r_1 \cdot byte_{2, i} \cdot 2^{32i} \right) \cdot s_2 + tn = z_1r_2 - z_2r_1 $$ $$ 0 \le byte_{1, i}, byte_{2, i} \le 255$$ and plug this into Inequality Solving with CVP repository. This gives us $db$ and it solves the problem.
tonality (30 solves)
Step 1 : Basic Analysis
- We get the ECDSA public key $P = dG$ and two messages.
- We can send a integer $t$, and we get the signature of first message signed with private key $td$.
- We now have to forge any signature of the second message with private key $d$.
Step 2 : Finding Attack Vector, and "Wishful Thinking"
There's nothing really going on in this problem, so we just need to use the first query very well.
Denote the two messages $m_0, m_1$ and their hashes $z_0, z_1$. Denote the integer we will send as $t$.
We will receive the signature $r_0, s_0$ such that the point $$ (z_0 / s_0) G + (r_0 / s_0) tP $$ has the first coordinate equal to $r_0$. Here, the integer division is done modulo $n$, the order of elliptic curve.
We now have to forge a signature $r_1, s_1$ such that the point $$ (z_1 / s_1) G + (r_1 / s_1)P$$ has the first coordinate equal to $r_1$. Here, the integer division is done modulo $n$, the order of elliptic curve.
We wish to solve this in the easiest way possible - and this will happen when $$ z_0/s_0 = z_1/s_1 , \quad (r_0 / s_0)t = (r_1/s_1), \quad r_0 = r_1$$ which can be rearranged as $$t = z_0 / z_1, \quad r_1 = r_0, \quad s_1 = z_1s_0/z_0$$ and submitting this to the server solves the problem.
story (32 solves)
Step 1 : Basic Analysis
- We have to send a sufficiently large UTF-8 string to the server.
- We receive the CRC16, CRC32, CRC64 values of the sent string back.
- We also receive the desired CRC16, CRC32, CRC64 values from the server.
- We have to make a string with the desired CRC values, with the same lowercase text as the original string.
Step 2 : Finding Attack Vector
The obvious problem is that CRCs are not meant to be an encryption of some sort. They satisfy the powerful relation $$crc(x) \oplus crc(y) \oplus crc(z) = crc(x \oplus y \oplus z)$$ which can be used to solve this problem relatively easily.
There are several ways to solve this problem, maybe even using finite field representation of CRC. However, I still think the method in Step 3 is much easier to deal with than dealing endian issues and figuring out which polynomial is actually used to compute CRC.
Step 3 : Exploiting with Linearity
Denote $x_{16}, x_{32}, x_{64}$ be the CRC values of "a" * 256.
Also, for each $0 \le i \le 255$, we denote $x'_{i, 16}, x'_{i, 32}, x'_{i, 64}$ as the CRC values of "a" * 256 but the $i$th 'a' is changed to 'A'.
These values can be computed by 257 server interactions, and the CRC computation is of course deterministic.
Now we can build the CRC values of any length 256 string with 'a' and 'A' only. We start with $x_{16}, x_{32}, x_{64}$, and if the $i$th character is 'A' instead of 'a', we XOR the values $x'_{i, 16} \oplus x_{16}, x'_{i, 32} \oplus x_{32}, x'_{i, 64} \oplus x_{64}$ to our CRC result.
Now changing 'a' to 'A' appropriately for the result CRC to match the target is something like a subset sum problem with bitstring XOR.
Of course, looking at each bit separately, this is nothing more than a system of linear equations over $\mathbb{F}_2$.
We solve this, find the locations where we have to change the lowercase/uppercase, and get the flag.
'CTF' 카테고리의 다른 글
| ACSC Crypto Writeups (0) | 2021.09.26 |
|---|---|
| CryptoCTF Writeups (DoRSA, Polish) (0) | 2021.08.05 |
| zer0lfsr 2021 Full Writeup (0CTF/TCTF 2021) (2) | 2021.07.05 |
| zer0lfsr 2021 Quick Solutions/Thoughts (0) | 2021.07.05 |
| LINE CTF Crypto Writeups (0) | 2021.03.22 |