|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
|
#!/usr/bin/sage
import hashlib
def solve_part1():
SUB_TABLE = set() # contains (a, b, c) such that a - b == c (mod p)
MUL_TABLE = set() # contains (a, b, c) such that a * b == c (mod p)
REGISTERED_EC = set() # contains elliptic curve points in y^2 = x^3 + 7 (mod p)
REGISTERED_X = set() # contains x-coordinates of a elliptic curve point of REGISTERED_EC
bn254 = 21888242871839275222246405745257275088696311157297823662689037894645226208583
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
x_start = int(input()) % p
y_start = int(input()) % p
assert (y_start * y_start) % p == (x_start * x_start * x_start + 7) % p
# this target value is the target x-coordinate
target = int.from_bytes(hashlib.sha256(str(x_start).encode() + b"#" + str(y_start).encode()).digest(), "big") % p
# (x_start, y_start) is known to be a valid elliptic curve point
REGISTERED_EC.add((x_start, y_start))
REGISTERED_X.add(x_start)
count = 0
while True:
count += 1
assert count < 20000
whi = int(input())
if whi == 1 or whi == 2:
a = int(input())
b = int(input())
quotient = int(input())
result = int(input())
assert 0 <= a < (1 << 256)
assert 0 <= b < (1 << 256)
assert 0 <= quotient < (1 << 256)
assert 0 <= result < (1 << 256)
if whi == 1:
# add (a, b, result) in SUB_TABLE
assert (a - b + p - quotient * p - result) % bn254 == 0
assert (a - b + p - quotient * p - result) % (1 << 256) == 0
SUB_TABLE.add((a, b, result))
if whi == 2:
# add (a, b, result) in MUL_TABLE
assert (a * b - quotient * p - result) % bn254 == 0
assert (a * b - quotient * p - result) % (1 << 256) == 0
MUL_TABLE.add((a, b, result))
if whi == 3:
# check two points (x1, y1), (x2, y2) are already registered elliptic curve points
# check (x3, y3) = (x1, y1) + (x2, y2) via elliptic curve addition
# valid computation over (mod p) is checked by SUB_TABLE and MUL_TABLE
x1 = int(input())
y1 = int(input())
x2 = int(input())
y2 = int(input())
assert (x1, y1) in REGISTERED_EC # check (x1, y1) is a known valid elliptic curve point
assert (x2, y2) in REGISTERED_EC # check (x2, y2) is a known valid elliptic curve point
lam = int(input())
if x1 == x2 and y1 == y2: # point doubling algorithm
x_sq = int(input())
x_sq_3 = int(input())
y_2 = int(input())
y_2_inv = int(input())
assert (x1, x1, x_sq) in MUL_TABLE # check x_sq = x1^2
assert (x_sq, 3, x_sq_3) in MUL_TABLE # check x_sq_3 = 3 * x1^2
assert (y1, 2, y_2) in MUL_TABLE # check y_2 = 2 * y1
assert (y_2, y_2_inv, 1) in MUL_TABLE # check y_2_inv = 1 / (2 * y1)
assert (x_sq_3, y_2_inv, lam) in MUL_TABLE # check lam = (3 * x1^2) / (2 * y1)
else:
y_diff = int(input())
x_diff = int(input())
x_diff_inv = int(input())
assert (y2, y1, y_diff) in SUB_TABLE # check y_diff = y2 - y1
assert (x2, x1, x_diff) in SUB_TABLE # check x_diff = x2 - x1
assert (x_diff, x_diff_inv, 1) in MUL_TABLE # check x_diff_inv = 1 / (x2 - x1)
assert (y_diff, x_diff_inv, lam) in MUL_TABLE # check lam = (y2 - y1) / (x2 - x1)
lam_sq = int(input())
lam_sq_minus_x1 = int(input())
x_final = int(input())
x1_minus_x_final = int(input())
lam_mul_x1_minus_x_final = int(input())
y_final = int(input())
assert (lam, lam, lam_sq) in MUL_TABLE # check lam_sq = lam^2
assert (lam_sq, x1, lam_sq_minus_x1) in SUB_TABLE # check lam_sq_minus_x1 = lam^2 - x1
assert (lam_sq_minus_x1, x2, x_final) in SUB_TABLE # check x_final = lam^2 - x1 - x2
assert (x1, x_final, x1_minus_x_final) in SUB_TABLE # check x1_minus_x_final = x1 - x_final
assert (lam, x1_minus_x_final, lam_mul_x1_minus_x_final) in MUL_TABLE # check lam_mul_x1_minus_x_final = lam * (x1 - x_final)
assert (lam_mul_x1_minus_x_final, y1, y_final) in SUB_TABLE # check y_final = lam * (x1 - x_final) - y1
REGISTERED_EC.add((x_final, y_final)) # add (x_final, y_final) to REGISTERED_EC
REGISTERED_X.add(x_final) # add x_final to REGISTERED_X
if whi == 4:
break
assert target in REGISTERED_X # end with the target x-coordinate in REGISTERED_X
def solve_part2():
ADD_TABLE = set() # contains (a, b, c) such that a + b == c (mod p)
MUL_TABLE = set() # contains (a, b, c) such that a * b == c (mod p)
# Curve25519
p = (1 << 255) - 19
E = EllipticCurve(GF(p), [0, 486662, 0, 1, 0])
G = E(GF(p)(9), GF(p)(43114425171068552920764898935933967039370386198203806730763910166200978582548))
# Commit a set of NUM_POINTS points in Curve25519
NUM_POINTS = 165
commit = bytes.fromhex(input().strip())
assert len(commit) == 32 * NUM_POINTS
# this is the target point on Curve25519
target = int.from_bytes(hashlib.sha256(commit).digest(), "big") * G
# Add tuples to ADD_TABLE and MUL_TABLE by submitting proofs
count = 0
while True:
count += 1
assert count < 20000
whi = int(input())
if whi == 1 or whi == 2:
a = int(input())
b = int(input())
quotient = int(input())
result = int(input())
assert 0 <= a < (1 << 256)
assert 0 <= b < (1 << 256)
assert 0 <= quotient < (1 << 256)
assert 0 <= result < (1 << 256)
if whi == 1:
assert (a + b - (quotient * p + result)) % (1 << 512) == 0
ADD_TABLE.add((a, b, result))
if whi == 2:
assert (a * b - (quotient * p + result)) % (1 << 512) == 0
MUL_TABLE.add((a, b, result))
if whi == 3:
break
# submit a bitmask corresponding to a subset
# the subset sum of the points you committed before must equal to the target point
bmask = int(input())
assert 0 <= bmask < (1 << NUM_POINTS)
tot = 0 * G
for i in range(NUM_POINTS):
if ((bmask >> i) & 1) == 0: # the bitmask doesn't contain the i'th point, so skip
continue
# the bitmask contains the i'th point
# decompress the 32 bytes, with proof, to obtain a point on Curve25519
x = int(input())
y = int(input())
top_value = int(input())
x_sq = int(input())
x_cube = int(input())
x_sq_486662 = int(input())
sum1 = int(input())
sum2 = int(input())
# x_sum is the x-coordinate encoded in the 32 byte compressed format
x_sum = 0
for j in range(32):
x_sum += commit[i * 32 + j] * (256 ** j)
x_sum &= ((1 << 255) - 1)
# bit is the parity of the y-coordinate encoded in the 32 byte compressed format
bit = (commit[i * 32 + 31] >> 7) & 1
assert x == x_sum # check x matches the encoded x-coordinate
assert 0 <= top_value < (1 << 255)
assert y == top_value * 2 + bit # check bit matches the parity of y
assert (x, x, x_sq) in MUL_TABLE # check x_sq = x^2
assert (x, x_sq, x_cube) in MUL_TABLE # check x_cube = x^3
assert (x_sq, 486662, x_sq_486662) in MUL_TABLE # check x_sq_486662 = 486662 * x^2
assert (x_cube, x_sq_486662, sum1) in ADD_TABLE # check sum1 = x^3 + 486662 * x^2
assert (sum1, x, sum2) in ADD_TABLE # check sum2 = x^3 + 486662 * x^2 + x
assert (y, y, sum2) in MUL_TABLE # check y^2 = x^3 + 486662 * x^2 + x, so (x, y) is in Curve25519
recovered_point = E(GF(p)(x), GF(p)(y))
tot += recovered_point # add the recovered point to the subset sum
assert tot == target # assert the subset sum matches the target point
solve_part1()
print("PART 1 SOLVED!")
solve_part2()
print("PART 2 SOLVED!")
flag = open("flag.txt", "r").read()
print(flag)
|
cs |
Part 1
You have access to proving subtraction and multiplication over $\mathbb{F}_p$, and using that, you can prove elliptic curve addition over secp256k1. From this, by using the provable elliptic curve addition, your goal is to provide $(x, y)$ inside secp256k1 such that you can provide a provable addition chain to the elliptic curve point with $H(x, y)$ as the x-coordinate. In other words, you need to find the discrete logarithm between $(x, y)$ and the point with $H(x, y)$ as the x-coordinate. Of course, raw discrete logarithm is hard in secp256k1.
The idea is in the faulty emulated finite field in the subtraction/multiplication proof.
Note that we are checking $a - b + p - q \cdot p - r = 0$ with the equation (here $l$ is the bn254 prime) $$a - b + p - q \cdot p - r \equiv 0 \pmod{l \cdot 2^{256}}$$ This isn't actually sound, as $q \cdot p$ can go as high as $2^{512}$, larger than the modulo of the equation above. Indeed, we can try $$a - b + p - q \cdot p + l \cdot 2^{256} = r$$ so in a way, we can get $r$ to be $l \cdot 2^{256} \pmod{p}$ more than what it's supposed to be. Similar ideas work for multiplication.
This allows us to do weird things with the elliptic curve addition - so we can try an invalid curve attack. As secp256k1 is of the form $y^2 = x^3 + b$, we can try to move to the curve $y^2 = x^3$, where discrete logarithm is easy as a finite field operation as the curve is singular. Now the goal would be to find the starting point on secp256k1 such that after a single attack on subtraction/multiplication, the point lies on $y^2 = x^3$. This can be written as a system of polynomial equations with $x, y$, so the usual tricks with resultants or Groebner basis, or even manual reduction to a single variable equation works. I used manual reduction, and rbtree used Groebner basis.
One of the solvers told me that a bruteforce for a smooth curve order ($p_{max} \approx 10^{15}$) worked, albeit painful.
The idea was taken by this vulnerability report in ZKP systems. See #2.
Part 2
You have to provide 165 points on Curve25519 in compressed form, and the hash of those points is the target point for subset sum. You then have to provide which of the 165 points will be the subset which sums to the target, while also providing the decompression proof that the compressed points decompress to the claimed result. Intuitively, $2^{165} \ll p$, so standard method doesn't work.
The main idea here is that $y$ can be larger than $p$. Therefore, if the $b$ is the bit and $y$ is the square root of $sum2$ that is less than $p$ with $b$ as its LSB, one can actually use $y' = 2p - y$ which also has $b$ as its LSB. However, as $y' \pmod{p} = p - y$, we see that $(x, y')$ and $(x, y)$ are different points. Using this, we can actually make three decisions for each point - not use it, use $y$, or use $y'$. Now $3^{165} \approx 2^{262} \gg p$.
Now this challenge is a puzzle: you have to find a set $S$ such that you can easily solve the modified subset sum $$\sum_S c_i s_i = T, \quad c_i \in \{-1,0,1\}$$ as the $3^n$ thing suggests, this can be solved via ternary systems, setting $s_i = 3^i$. See balanced ternary systems.
There is a catch - you need to prove that $(2p - y)^2 \equiv sum2 \pmod{p}$. To do so, you need to provide $0 \le q < 2^{256}$ such that $$(2p-y)^2 = q \cdot p + sum2$$ which means that $$2p-y < \sqrt{2^{256} \cdot p} \approx \sqrt{2} p$$ forcing $y > (2 - \sqrt{2})p \approx 0.6p$. Therefore, this technique doesn't work for all $y$.
This can be resolved as follows. Select the $i$th point as $3^i \cdot v_i \cdot G$ where $v_i$ is small positive integer, and not a multiple of $3$.
In this case, solving subset sum to $N$ with values $v_0, 3v_1, 9v_2, \cdots$ can be done recursively as follows
- if $N \equiv 0 \pmod{3}$, solve $N/3$ with $v_1, 3v_2, 9v_3, \cdots$
- if $N \equiv v_0 \pmod{3}$, solve $(N-v_0)/3$ with $v_1, 3v_2, 9v_3, \cdots$
- if $N \equiv -v_0 \pmod{3}$, solve $(N+v_0)/3$ with $v_1, 3v_2, 9v_3, \cdots$
as we can see, the value of $N$ decreases exponentially - so at some point, the value of $N$ will become small regardless - say, within $[-40, 40]$. The unfortunate part is that we don't know if it will become exactly zero. In practice, it turns out that $N$ does become zero.
Here, we show a much more intuitively sound way for a finish. Since $3^{163}$ is sufficiently large, what we can do is to do the $3^i \cdot v_i \cdot G$ for $0 \le i < 164$, but set the final 164th point to be a random elliptic curve point. This point will not be used for subset sum, but it will be used to try out various target points, as the target point is the hash of the entire set of 165 points. This way, we can try various target points, and clearly with a sufficient probability we will be able to find a target point in which $N$ does become exactly zero.
An alternate way by Mystiz is to have use $v_0, 3v_0, \cdots 3^{14} v_0, v_1, 3v_1, \cdots, 3^{14} v_1, \cdots v_{10}, \cdots, 3^{14} v_{10}$ and so on - then, one can try to solve for $\sum_{i=0}^{10} c_i v_i = T$ with small coefficients $c_i$ via LLL. Here, the catch is that $3^0 v_i, 3^1 v_i, \cdots, 3^{14} v_i$ must have working set of $y$-coordinates, but since there's only 15 points this actually works with high probability. Note that while we mentioned $y > 0.6p$, we can also handle $y < 0.4p$ using $p+y$ and $p-y$. Therefore, only 20% of the points fail to use this trick, and $0.8^{15}$ is definitely brute-forcable.
The idea was taken by this vulnerability report in ZKP systems. See #9.
'CTF' 카테고리의 다른 글
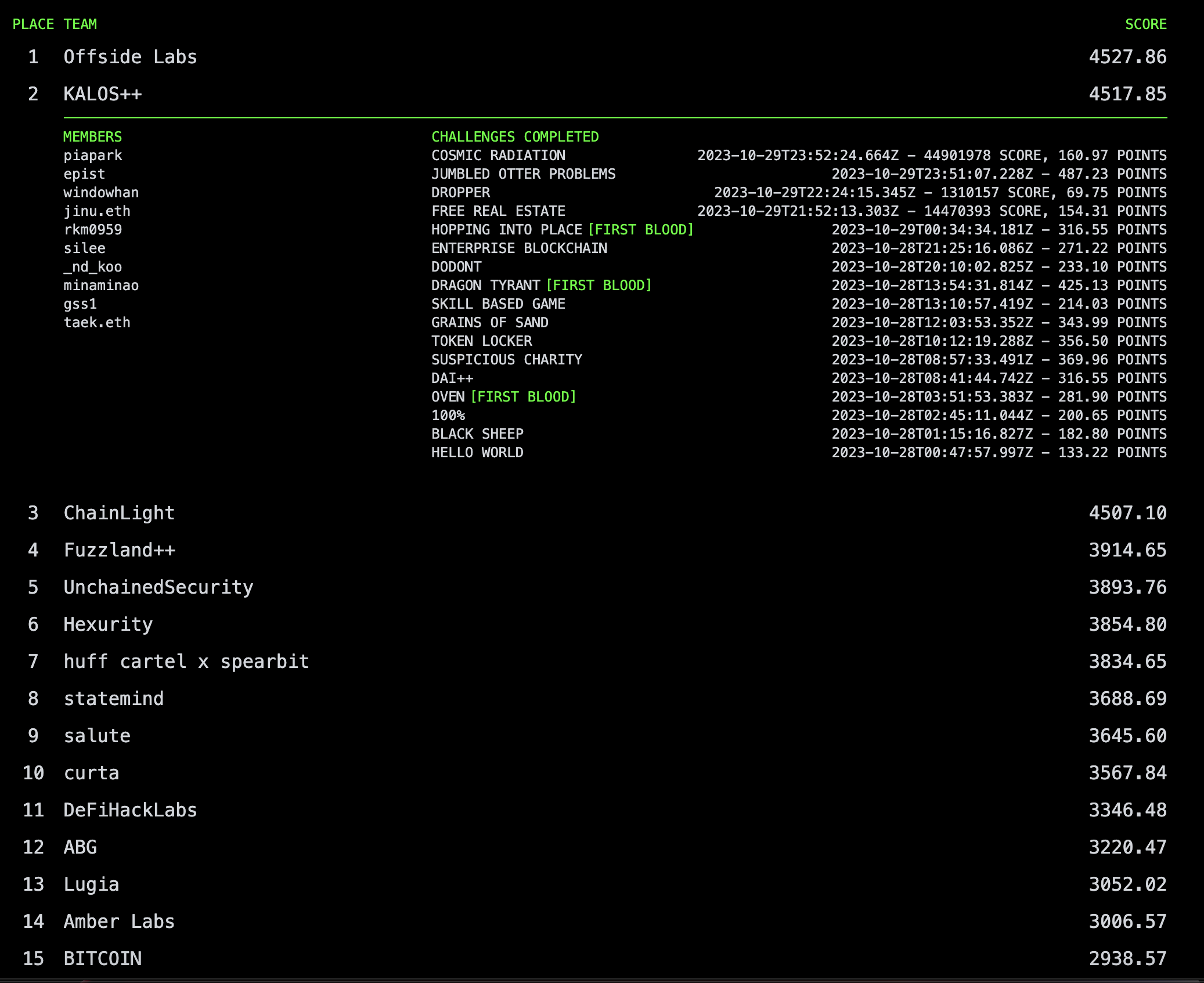
| Paradigm CTF 2023 2nd Place (0) | 2023.10.31 |
|---|---|
| CODEGATE 2023 Finals - The Leakers (1 solve) (1) | 2023.08.25 |
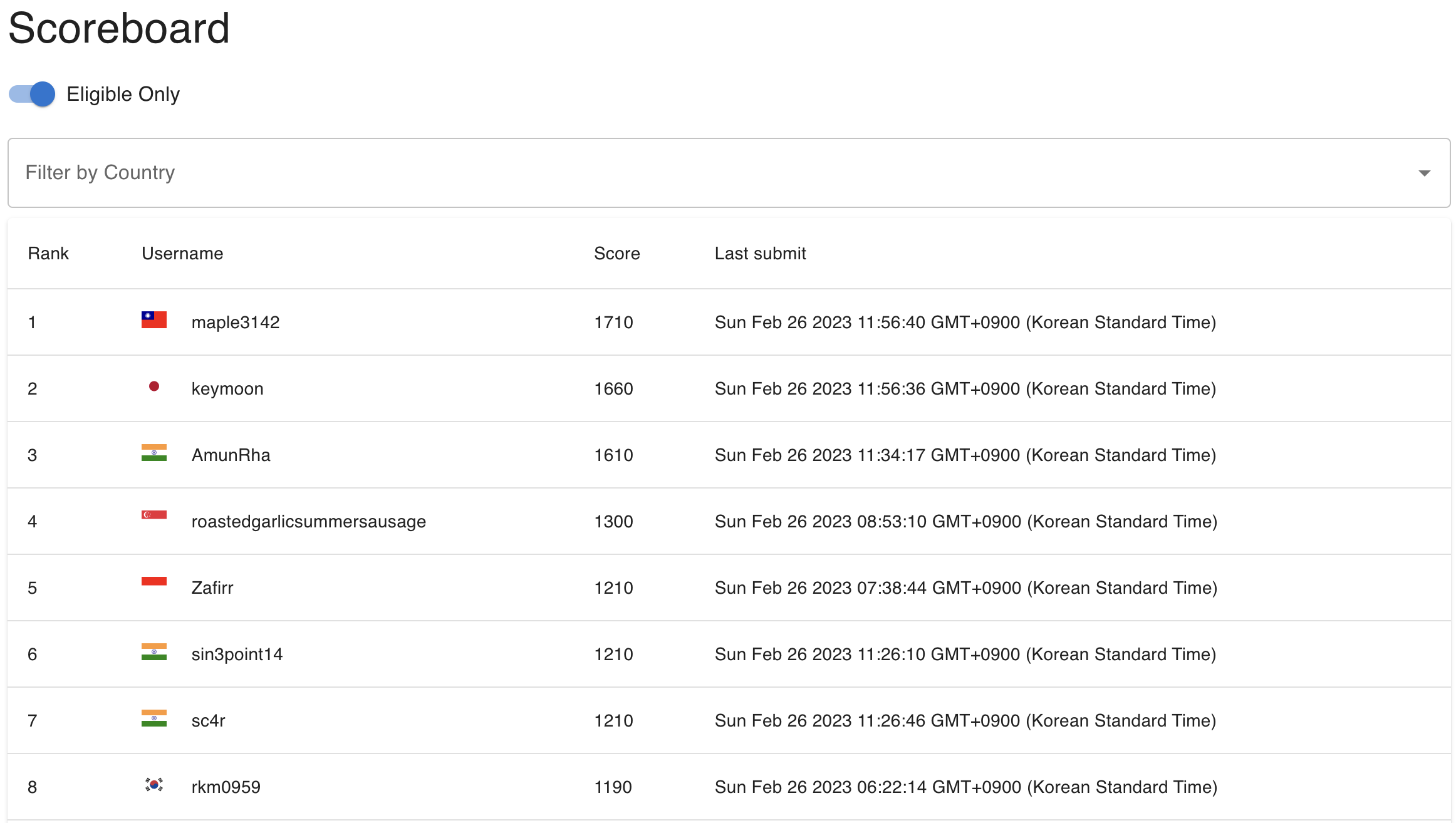
| ACSC 2023 Writeups (0) | 2023.02.26 |
| HackTM CTF Writeup (0) | 2023.02.22 |
| BlackHat MEA Finals (0) | 2022.11.21 |